Фибоначчиева система счисления: различия между версиями
w>Incnis Mrsi (Кнут, Кнут… я сам немного подумал, и понял, в чём тут дело!) |
w>Incnis Mrsi |
||
| Строка 1: | Строка 1: | ||
'''[[Фибоначчи]]ева система счисления''' — [[позиционная система счисления]] для [[целое число|целых чисел]] на основе [[числа Фибоначчи|чисел Фибоначчи]] F<sub>2</sub>=1, F<sub>3</sub>=2, F<sub>4</sub>=3, F<sub>5</sub>=5, F<sub>6</sub>=8 и т.д. | '''[[Фибоначчи]]ева система счисления''' — [[позиционная система счисления]] для [[целое число|целых чисел]] на основе [[числа Фибоначчи|чисел Фибоначчи]] F<sub>2</sub>=1, F<sub>3</sub>=2, F<sub>4</sub>=3, F<sub>5</sub>=5, F<sub>6</sub>=8 и т.д. | ||
| − | |||
| − | |||
{| align=right class=standard cellpadding=6 style="margin-left: 20px" | {| align=right class=standard cellpadding=6 style="margin-left: 20px" | ||
| + | | colspan=3 |[[Image:Zeckendorf representations.png|320px]] | ||
| + | |- | ||
!Число | !Число | ||
!Запись<br>в ФСС | !Запись<br>в ФСС | ||
| Строка 13: | Строка 13: | ||
| align=right |F<sub>2</sub>=1 | | align=right |F<sub>2</sub>=1 | ||
| align=right |<tt>1</tt> | | align=right |<tt>1</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>1<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |F<sub>3</sub>=2 | | align=right |F<sub>3</sub>=2 | ||
| align=right |<tt>10</tt> | | align=right |<tt>10</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>01<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |F<sub>4</sub>=3 | | align=right |F<sub>4</sub>=3 | ||
| align=right |<tt>100</tt> | | align=right |<tt>100</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>001<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |4 | | align=right |4 | ||
| align=right |<tt>101</tt> | | align=right |<tt>101</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>101<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |F<sub>5</sub>=5 | | align=right |F<sub>5</sub>=5 | ||
| align=right |<tt>1000</tt> | | align=right |<tt>1000</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>0001<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |6 | | align=right |6 | ||
| align=right |<tt>1001</tt> | | align=right |<tt>1001</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>1001<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |7 | | align=right |7 | ||
| align=right |<tt>1010</tt> | | align=right |<tt>1010</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>0101<font color=#B20080>1</font></tt> |
|- | |- | ||
| align=right |F<sub>6</sub>=8 | | align=right |F<sub>6</sub>=8 | ||
| align=right |<tt>10000</tt> | | align=right |<tt>10000</tt> | ||
| − | | align=left |<tt> | + | | align=left |<tt>00001<font color=#B20080>1</font></tt> |
|- | |- | ||
| colspan=3 align=center |… | | colspan=3 align=center |… | ||
| Строка 47: | Строка 47: | ||
|F<sub>n</sub>-1 | |F<sub>n</sub>-1 | ||
|<tt> 101010</tt>… | |<tt> 101010</tt>… | ||
| − | | align=right |…<tt> | + | | align=right |…<tt>010101<font color=#B20080>1</font> </tt> |
|- | |- | ||
|F<sub>n</sub> | |F<sub>n</sub> | ||
|<tt>10</tt>……<tt>00</tt> | |<tt>10</tt>……<tt>00</tt> | ||
| − | | align=right |<tt>00</tt>……<tt> | + | | align=right |<tt>00</tt>……<tt>01<font color=#B20080>1</font></tt> |
|- | |- | ||
|F<sub>n</sub>+1 | |F<sub>n</sub>+1 | ||
|<tt>10</tt>……<tt>01</tt> | |<tt>10</tt>……<tt>01</tt> | ||
| − | | align=right |<tt>10</tt>……<tt> | + | | align=right |<tt>10</tt>……<tt>01<font color=#B20080>1</font></tt> |
| − | |||
| − | |||
|} | |} | ||
| + | |||
| + | == Представление натуральных чисел == | ||
Любому неотрицательному целому числу <math>a = 0,\ 1,\ 2,\dots</math> можно единственным образом представить через последовательность [[бит]]ов …ε<sub>k</sub>…ε<sub>4</sub>ε<sub>3</sub>ε<sub>2</sub>: <math>a = \sum_k \varepsilon_k F_k,\ \varepsilon_k = 0,1</math>, причём последовательность {ε<sub>k</sub>} содержит лишь конечное число единиц, и не имеет пар соседних единиц: <math>\forall k\ge 2: (\varepsilon_k=1) \Rightarrow (\varepsilon_{k+1}=0)</math>. | Любому неотрицательному целому числу <math>a = 0,\ 1,\ 2,\dots</math> можно единственным образом представить через последовательность [[бит]]ов …ε<sub>k</sub>…ε<sub>4</sub>ε<sub>3</sub>ε<sub>2</sub>: <math>a = \sum_k \varepsilon_k F_k,\ \varepsilon_k = 0,1</math>, причём последовательность {ε<sub>k</sub>} содержит лишь конечное число единиц, и не имеет пар соседних единиц: <math>\forall k\ge 2: (\varepsilon_k=1) \Rightarrow (\varepsilon_{k+1}=0)</math>. | ||
За исключением последнего свойства, данное представление аналогично [[двоичная система счисления|двоичной системе счисления]]. | За исключением последнего свойства, данное представление аналогично [[двоичная система счисления|двоичной системе счисления]]. | ||
| Строка 69: | Строка 69: | ||
=== Использование в теории информации === | === Использование в теории информации === | ||
На основе фибоначчиевой системы счисления строится ''код (кодирование) Фибоначчи'' — [[универсальный код (сжатие данных)|универсальный код]] для натуральных чисел (1, 2, 3…), использующий последовательности [[бит]]ов. Поскольку комбинация <tt>11</tt> запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. | На основе фибоначчиевой системы счисления строится ''код (кодирование) Фибоначчи'' — [[универсальный код (сжатие данных)|универсальный код]] для натуральных чисел (1, 2, 3…), использующий последовательности [[бит]]ов. Поскольку комбинация <tt>11</tt> запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. | ||
| − | Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз <tt>1</tt> (см. таблицу). | + | Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз <tt>1</tt> (см. таблицу). То есть, кодовая последовательность имеет вид: |
| + | : ε<sub>2</sub>ε<sub>3</sub>…ε<sub>''n''</sub><font color=#B20080>1</font>, | ||
| + | где ''n'' — номер самого старшего разряда с единицей. | ||
| + | |||
| + | === Арифметика === | ||
| + | При сложении чисел в позиционных системах счисления приходится выполнять ''перенос'', то есть устранять последствия [[арифметическое переполнение|переполнения]] разряда. Например, в двоичной системе: <span style="background-color: rgb(255,255,51)">01</span> + <span style="background-color: rgb(255,255,51)">01</span> = <span style="background-color: rgb(255,255,51)">0<font color=red>2</font></span> = <span style="background-color: rgb(255,255,51)">10</span>. В фибоначчиевой системе дело обстоит намного сложнее. Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только вправо, но и влево: <span style="background-color: rgb(102,255,51)">0<font color=red>2</font>00</span> = <span style="background-color: rgb(102,255,51)">1001</span>. При переносе в отсутствующие разряды ε<sub>1</sub> и ε<sub>0</sub> следует помнить, что F<sub>1</sub>=1=F<sub>2</sub> и F<sub>0</sub>=0. Во-вторых, требуется избавляться от соседних единиц: <span style="background-color: rgb(102,255,51)">0<font color=red>11</font></span> = <span style="background-color: rgb(102,255,51)">100</span>. Правило для раскрытия двоек является следствием этого равенства: <span style="background-color: rgb(102,255,51)">0<font color=red>2</font>00</span> = <span style="background-color: rgb(102,255,51)">0100</span> + <span style="background-color: rgb(102,255,51)">00<font color=red>11</font></span> = <span style="background-color: rgb(102,255,51)">0<font color=red>11</font>1</span> = <span style="background-color: rgb(102,255,51)">1001</span>. | ||
| + | |||
| + | {{section-stub}} | ||
== Обобщение на действительные числа == | == Обобщение на действительные числа == | ||
Похожее устройство имеет позиционная система счисления для [[действительные числа|действительных чисел]], основанием которой служит [[золотое сечение]] <math>\varphi = (1 + \sqrt{5})/2</math> — [[иррациональное число]]. | Похожее устройство имеет позиционная система счисления для [[действительные числа|действительных чисел]], основанием которой служит [[золотое сечение]] <math>\varphi = (1 + \sqrt{5})/2</math> — [[иррациональное число]]. | ||
| − | Оказывается, что любое действительное число '' | + | Оказывается, что любое действительное число ''x'' из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения: |
| − | : <math> | + | : <math>x = \sum_{k=-1}^{-\infty} \varepsilon_k \varphi^k,\ \varepsilon_k = 0,1\ ,</math> |
где {ε<sub>k</sub>} обладает тем же свойством отсутствия соседних единиц. | где {ε<sub>k</sub>} обладает тем же свойством отсутствия соседних единиц. | ||
| + | Коэффициенты находятся последовательным сравнением ''x'' с <math>\varphi^{-1}</math> — золотым сечением отрезка [0,1], вычитанием <math>\varphi^{-1}</math> (если ε<sub>k</sub>=1) и умножением на <math>\varphi</math>. | ||
Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение: | Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение: | ||
: <math>a = \sum_{k=N-1}^{-\infty} \varepsilon_k \varphi^k\,,</math> | : <math>a = \sum_{k=N-1}^{-\infty} \varepsilon_k \varphi^k\,,</math> | ||
где ''N'' таково, что <math>a < \varphi^N</math>. | где ''N'' таково, что <math>a < \varphi^N</math>. | ||
| − | Разумеется, следует считать что <math>\varepsilon_k = 0</math> для <math>k \ge N</math>. | + | Разумеется, следует считать что <math>\varepsilon_k = 0</math> для всех <math>k \ge N</math>. |
| + | {| align=left class=standard style="margin-right: 20px" | ||
| + | |- | ||
| + | ! Число | ||
| + | ! Представление<br>через<br>степени <math>\varphi</math> | ||
| + | |- | ||
| + | | 1 | ||
| + | |<tt> 1,</tt> | ||
| + | |- | ||
| + | | 2 | ||
| + | |<tt> 10,01</tt> | ||
| + | |- | ||
| + | | 3 | ||
| + | |<tt> 100,01</tt> | ||
| + | |- | ||
| + | | 4 | ||
| + | |<tt> 101,01</tt> | ||
| + | |- | ||
| + | | 5 | ||
| + | |<tt> 1000,1001</tt> | ||
| + | |- | ||
| + | | 6 | ||
| + | |<tt> 1010,0001</tt> | ||
| + | |- | ||
| + | | 7 | ||
| + | |<tt> 10000,0001</tt> | ||
| + | |- | ||
| + | | 8 | ||
| + | |<tt> 10001,0001</tt> | ||
| + | |- | ||
| + | | 9 | ||
| + | |<tt> 10010,0101</tt> | ||
| + | |- | ||
| + | |10 | ||
| + | |<tt> 10100,0101</tt> | ||
| + | |- | ||
| + | |11 | ||
| + | |<tt> 10101,0101</tt> | ||
| + | |- | ||
| + | |12 | ||
| + | |<tt>100000,101001</tt> | ||
| + | |- | ||
| + | |13 | ||
| + | |<tt>100010,001001</tt> | ||
| + | |- | ||
| + | |14 | ||
| + | |<tt>100100,001001</tt> | ||
| + | |} | ||
Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. | Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. | ||
| − | Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент [[кольцо (алгебра)|кольца]] <math>{\mathbb Z}+\varphi{\mathbb Z}</math>) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.<!-- тут хорошо бы найти источник --> | + | Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент [[кольцо (алгебра)|кольца]] <math>{\mathbb Z}+\varphi{\mathbb Z}</math>) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.<ref>[[:en:Golden ratio base]]{{ref-en}}<!-- тут хорошо бы найти настоящий источник --></ref> |
Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств: | Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств: | ||
: <math>F_k = F_{k-1} + F_{k-2}\,,\ \varphi^k = \varphi^{k-1} + \varphi^{k-2}\,,</math> | : <math>F_k = F_{k-1} + F_{k-2}\,,\ \varphi^k = \varphi^{k-1} + \varphi^{k-2}\,,</math> | ||
позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.<!-- тут надо уточнить, на самом деле связь будет с некоторыми оговорками и с точностью до множителя √5 или что-то такое --Incnis Mrsi --> | позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.<!-- тут надо уточнить, на самом деле связь будет с некоторыми оговорками и с точностью до множителя √5 или что-то такое --Incnis Mrsi --> | ||
| − | + | ||
| + | Правила сложения аналогичны показанным [[#Арифметика|выше]] с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение. | ||
== Фибоначчиево «произведение» == | == Фибоначчиево «произведение» == | ||
| Строка 97: | Строка 153: | ||
: <math>a\circ b = 3 a b - a [\varphi^{-2}(b+1)] - b [\varphi^{-2}(a+1)]\ ,</math> где […] — [[целая часть]]. | : <math>a\circ b = 3 a b - a [\varphi^{-2}(b+1)] - b [\varphi^{-2}(a+1)]\ ,</math> где […] — [[целая часть]]. | ||
| − | Эта операция обладает [[ассоциативность]]ю. | + | Эта операция обладает [[ассоциативность]]ю. <!-- |
| − | + | Доказательство не такое простое, тут надо думать. | |
| − | Впервые на ассоциативность этой операции обратил внимание [[Дональд Кнут]]. | + | --Incnis Mrsi --> |
| − | Следует отметить, что другое «произведение» <math>\sum_{k,l} \varepsilon_k \zeta_l F_{k+l-2},</math> отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно | + | Впервые на ассоциативность этой операции обратил внимание [[Дональд Кнут]]<ref> D. E. Knuth, Fibonacci multiplication, Appl. Math. Lett. 1 (1988), 57-60.</ref>. |
| + | Следует отметить, что другое «произведение» <math>\sum_{k,l} \varepsilon_k \zeta_l F_{k+l-2},</math> отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно. | ||
{{section-stub}} | {{section-stub}} | ||
| Строка 110: | Строка 167: | ||
[[Категория:Системы счисления]] | [[Категория:Системы счисления]] | ||
[[Категория:Золотое сечение]] | [[Категория:Золотое сечение]] | ||
| + | [[Категория:Сжатие данных]] | ||
[[en:Fibonacci coding]] | [[en:Fibonacci coding]] | ||
[[eo:Vikipedio:Projekto matematiko/Fibonacci-a kodigo]] | [[eo:Vikipedio:Projekto matematiko/Fibonacci-a kodigo]] | ||
[[fr:Codage de Fibonacci]] | [[fr:Codage de Fibonacci]] | ||
Версия от 19:05, 4 января 2009
Фибоначчиева система счисления — позиционная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д.
| ||
| Число | Запись в ФСС |
Код Фибоначчи |
|---|---|---|
| 0 | 0……0 | |
| F2=1 | 1 | 11 |
| F3=2 | 10 | 011 |
| F4=3 | 100 | 0011 |
| 4 | 101 | 1011 |
| F5=5 | 1000 | 00011 |
| 6 | 1001 | 10011 |
| 7 | 1010 | 01011 |
| F6=8 | 10000 | 000011 |
| … | ||
| Fn-1 | 101010… | …0101011 |
| Fn | 10……00 | 00……011 |
| Fn+1 | 10……01 | 10……011 |
Представление натуральных чисел
Любому неотрицательному целому числу можно единственным образом представить через последовательность битов …εk…ε4ε3ε2: , причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц: . За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование
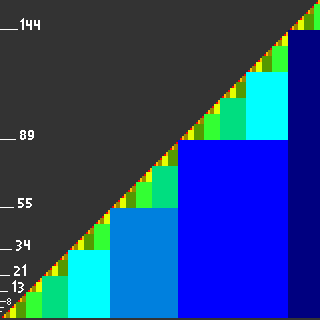
В основе лежит теорема Цеккендорфа — любое неотрицательное целое число представимо в виде суммы некоторого набора чисел Фибоначчи, не содержащего пары соседних чисел Фибоначчи. Причём представление такое единственно.
Доказательство существования легко провести по индукции. Любое целое число попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого верно неравенство: . Таким образом, , где , так что разложение числа уже не будет содержать слагаемого .
Использование в теории информации
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид:
- ε2ε3…εn1,
где n — номер самого старшего разряда с единицей.
Арифметика
При сложении чисел в позиционных системах счисления приходится выполнять перенос, то есть устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10. В фибоначчиевой системе дело обстоит намного сложнее. Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только вправо, но и влево: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что F1=1=F2 и F0=0. Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства: 0200 = 0100 + 0011 = 0111 = 1001.
Обобщение на действительные числа
Похожее устройство имеет позиционная система счисления для действительных чисел, основанием которой служит золотое сечение — иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения: где {εk} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с — золотым сечением отрезка [0,1], вычитанием (если εk=1) и умножением на . Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение: где N таково, что . Разумеется, следует считать что для всех .
| Число | Представление через степени |
|---|---|
| 1 | 1, |
| 2 | 10,01 |
| 3 | 100,01 |
| 4 | 101,01 |
| 5 | 1000,1001 |
| 6 | 1010,0001 |
| 7 | 10000,0001 |
| 8 | 10001,0001 |
| 9 | 10010,0101 |
| 10 | 10100,0101 |
| 11 | 10101,0101 |
| 12 | 100000,101001 |
| 13 | 100010,001001 |
| 14 | 100100,001001 |
Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент кольца ) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[1]
Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств: позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.
Правила сложения аналогичны показанным выше с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение.
Фибоначчиево «произведение»
Для целых чисел и можно определить «произведение»[2] формула для которого аналогична формуле умножения двоичных чисел.
Разумеется, данная операция не является настоящим умножением чисел, и выражается[3] формулой: где […] — целая часть.
Эта операция обладает ассоциативностью. Впервые на ассоциативность этой операции обратил внимание Дональд Кнут[4]. Следует отметить, что другое «произведение» отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно. Шаблон:Section-stub
Источники
- «Коды Фибоначчи», факультет информационных технологий и программирования ИТМО
- «Код Фибоначчи» на Викизнании
- ↑ en:Golden ratio base (англ.)
- ↑ Шаблон:OEIS2C, en:Zeckendorf's theorem (англ.)
- ↑ Notes on the Fibonacci circle and arroba products (англ.)
- ↑ D. E. Knuth, Fibonacci multiplication, Appl. Math. Lett. 1 (1988), 57-60.
en:Fibonacci coding eo:Vikipedio:Projekto matematiko/Fibonacci-a kodigo fr:Codage de Fibonacci